HanLab_Logo

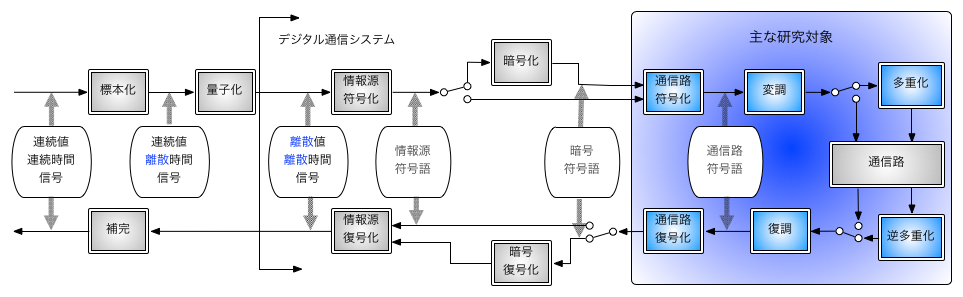
情報通信の目的は，情報をより速く希望の相手に正確に伝えることです．しかし，送信機から送信された信号は伝搬途中で電力減衰と共に，通信路の帯域制限による信号歪みが生じます． また，受信機で加わる雑音，反射波によるフェージングとシンボル間干渉や複数のユーザが通信路を共有する際に生じ得るマルチアクセス干渉なども 通信システムの性能を劣化させる原因となりますが，高速移動時にはドップラー効果による周波数偏移が更に安定した高速通信を困難にします．

情報通信理論は，情報理論と通信理論で構成されてますが，この二つの分野は共通のテーマが多くあります．大雑把に分けて，情報理論では様々な通信環境においての通信の限界について調べますが，確率統計に関する知識が不可欠です． 一方，通信理論では具体的な通信方法について検討し，その性能分析や改善策について考えます． 必要となる数学知識は，確率統計の他，微積分，線形代数，確率過程，信号解析及び信号処理などがあります．

変復調や帯域制限のため，どんなディジタル通信システムも通信速度を上げるに従って符号間干渉の問題が厳しくなって来ます．このテーマでは，この影響を軽減するための波形整形，等化などの問題について調べます．
IA
無線通信などでは図で示したように複数のユーザが同じ通信路を通じで同時に通信を行ないますが， このような通信システムはマルチアクセス通信路(Multiple-Access Channel)と呼ばれます． MAC通信では，ユーザ間の信号が互いに干渉し合うのを回避するために，送信時間をずらしたり， 各ユーザに異なる周波数を割り当てたりする直行分割方式で通信を行いますが， 直行分割方式ではK人のユーザがいる場合各ユーザは1/Kの資源しか割り当てられません． 一方，送信機で通信路の干渉状況が分かっている場合には，干渉整列の方式で通信を行うと， すべてのユーザが最大で1/2の資源を利用できる可能性があります． このテーマでは，与えられた通信路状況をいかに有効に利用するかについて考えます．
従来，通信の物理層は通信理論に基づいて慎重に設計してきました．しかし，近年深層学習を応用した人工知能が急速に発展し，通信システムの物理層においてもその応用可能性が検討されています． 本テーマでは，送受信機で学習データを用いた深層学習の適応について研究します．

送信機より送信された情報は，雑音や干渉の影響で誤って受信機に伝達されることがありますが，デジタル通信方式では誤り訂正符号を適応することで許容範囲内の誤りなら訂正することができます．

通信路符号化もしくは符号理論と呼ばれる分野は，このような誤り訂正符号の構成法と情報復元方法に関して研究しますが，なるべく多くの情報を送れる符号化レートが高く， 誤り訂正能力が優れ，情報復元が簡単な符号を見つけることを目標とします． 必要となる数学知識は，確率統計，微積分，線形代数，有限体理論などがあります．

過去の送信情報とは無関係に，一つあるひは複数のビットを特定の符号語にマッピングする符号をブロック符号と呼びます．線形ブロック符号であるRS符号は，符号化が簡単な回路で実装でき，効率的な復号方法が見つかっている符号です． RS符号は特に，誤りが集中的に起きるバーストエラーへの訂正能力に優れ，下記の畳込み符号と連結しての応用も多くあります．

過去の送信情報と無関係に符号語を生成するブロック符号と比べて，生成される符号語が過去一定期間の送信情報と現在の入力情報に依存する符号は有限状態機械(Finite State Machine)として考えられ， 有向グラフを用いて表現できます．有限状態符号器を用いるトレリス符号の中で，特に線形となる畳み込み符号は，携帯や無線LANなどで広く使われている符号でありますが， このテーマではフェージング環境においてそれぞれの無線通信システムでの適応方法について研究します．

複数の畳込み符号をインターリーバで繋いで構成するTurbo符号は，ビット誤りを生じさせずに伝送できる最大の伝送速度（理論可能な限界値）に近い特性を有した上に， 符号化や復号化が簡単であることより，移動通信企画に採用されています．このテーマでは，与えられた畳み込み符号に適するインターリーバの設計を中心に，Turbo符号の新たな展開を研究します．
LDPCは，シャノン限界に近い情報伝送レートを達成できる符号で，1963年に開発されてから近年になって再び注目を浴びています． その理由には，確率のグラフィカルモデルに基づいた確率伝搬法(Belief Propagation)あるいはSum-productメッセージ伝達法（sum-product message passing）と呼ばれる復号アルゴリズムの開発が大きく貢献しています． 確率のグラフィカルモデルの手法は，人工知能や機械学習など様々な分野で広く応用されています．

通信路符号化を行った情報を電話線や無線電波を介して送信するには，対応した通信媒体での伝送に適した形に変換する必要がありますが，その役割を担うのが変調方式です．

変調方式の分野では，送信エネルギーと通信媒体の帯域を有効に使うために，送信するビットと波形の効率的な対応方法について研究しますが，主に確率統計，微積分，幾何学などの数学的道具を使用します．

送信機は，送信ビット列に応じて送信する波形の振幅，周波数及び位相を変化させることで，受信機に情報を伝えます． そのときに，どんな送信ビット列をどんな波形に対応させるかによって，送信に必要な平均電力と雑音や通信路フェージングに対する耐性が大きく変わります． この研究では，様々な通信システムと通信環境を想定して，送信エネルギーと通信媒体の帯域を有効に使うための送信ビット列と波形の対応方法について研究します．
主にディジタル衛星放送やディジタル地上放送で使われている符号化変調方式は，この方式では誤り訂正符号化技術と変調技術を一体化させることによって，今までと同じ信号点エネルギーで同等の誤り訂正能力を持たせたまま一度により多くの情報を送れるようになります． つまり，限られた周波数帯域と信号電力で，より高速かつ信頼性の高い通信が行なえるようになりますが，本研究では，変調方式によって送信可能な信号点の構成方法や信号点と符号化された系列の対応関係を決定するアルゴリズムについての研究を行ないます．
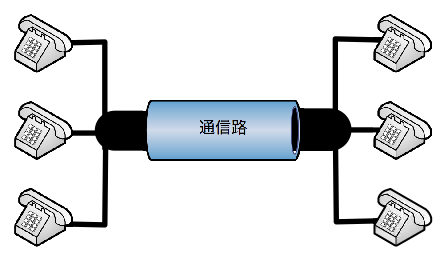
Multiplexing

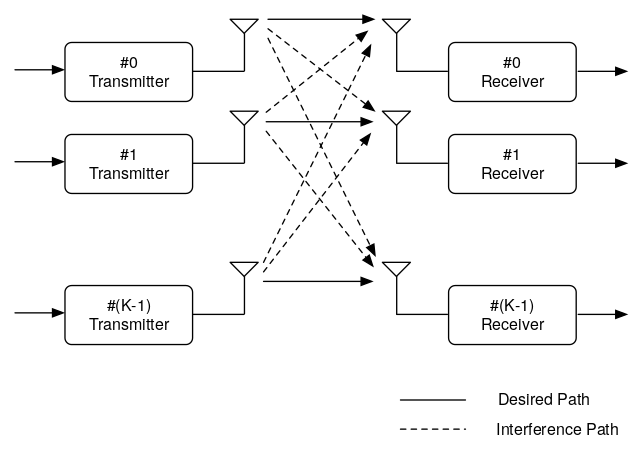
たくさんのユーザをつなぐ通信網において，ユーザペアごとに電話線を引いて回線を設置するには莫大なコストがかかり現実的ではありません．それで，実際の電話回線やインターネット通信網では単一の基幹通信路を複数のユーザが共有し， 送信時には届ける情報そのもの以外に，誰に届ける情報なのかが区別できる「住所情報」を埋め込む必要がありますが，その具体的な実現方法を多重化方式或いは多重アクセス(multiacess)と呼びます．

我々が使っている携帯電話の無線通信は，今まで多重化方式によって第一世代(1G:Analog方式)，第一世代(1G:Analog方式)，第二世代(2G:TDMA方式)，第三世代(3G:CDMA方式)，第四世代(4G:OFDMA方式)と区分しています．

CDMA
CDMA(Code Division Multiple Access)は，各ユーザに固有の拡散符号を割り当てて多元接続を行う方式であり，スペクトル拡散通信とも呼ばれています． CDMA は音声だけでなく静止画像・動画・コンピュータデータなどの各メディアに柔軟に対応できるため，21世紀の第三世代移動体通信(IMT-2000)採用されましたが，通信路間干渉が問題で第四移動体通信規格からは外されました． しかし，低遅延などの特性がIoTなどの応用に適しているとみなされ，第五世代(5G)ではNOMAとして再び注目を浴びています． 本研究では，通信全体の効率を上げるために，通信路間干渉がないCDMA，NOMA，同期CDMAなどについて研究しています．
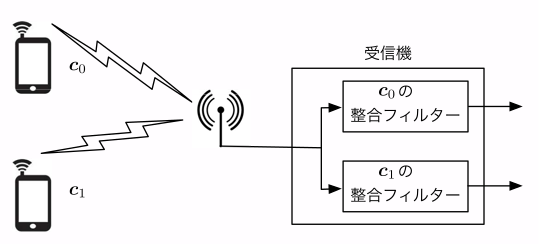
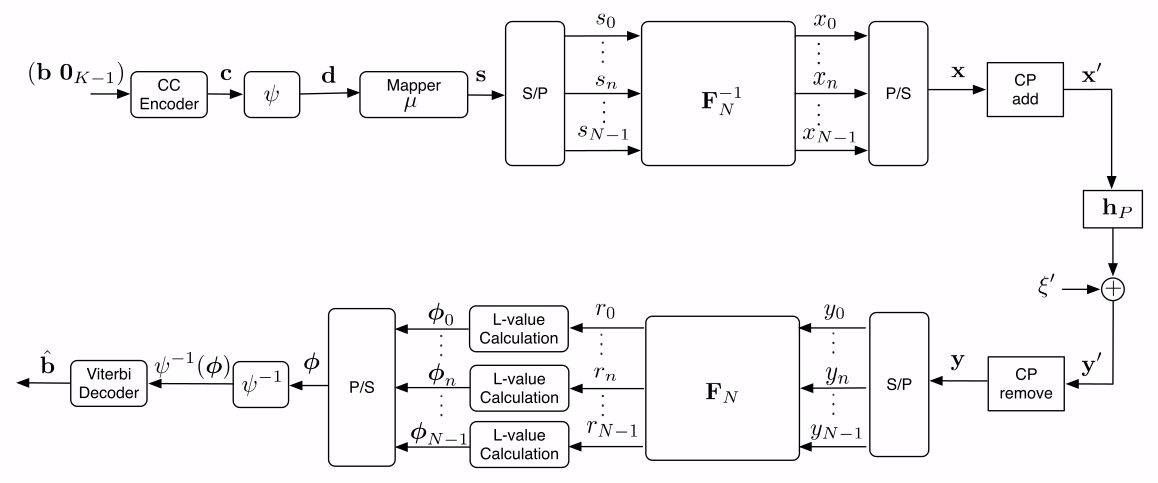
COFDM
PSKやQAMなどのディジタル変復調は単一搬送波で伝送されますが，無線LANやデジタル放送で使われているOFDMでは直交関係にある複数の搬送波を互いに重畳させてデータ伝送を行います． OFDMは反射波が存在する無線環境で通信路等化が簡単になる長所がありますが，誤り訂正符号を適応しないと通信性能が悪く，平均電力対ピーク電力比(PAPR)が高いとの欠点もあります． ここでは，主にOFDMに誤り訂正を加えたCOFDMの性能向上方法について研究しています．
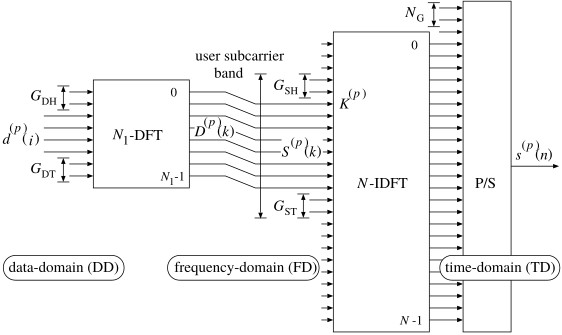
SCFDMA
SC-FDMA方式は，QAMなどのディジタル変調信号をDFT行列で拡散してからOFDMの連続した副搬送波を介して送信する伝送方式ですが，OFDM方式に比べてPAPRが低く，通信性能も良くなることから LTE(Long term evaluation)では，移動端末から基地局の上り回線規格に採用されています．本研究では，高速移動時のドップラー周波数偏移に起因する干渉の分析し，その抑制策などについて考えています．
光空間伝搬を用いた通信はビル間や室内のデータ伝送，電話，路車間通信などに実用化されています．光無線LANは法規制がないため，光搬送波の持つ広帯域が自由に利用できます． 光搬送波は室内の壁や天井で完全に反射してしまうため，隣接ネットワークとの干渉が起こりません．従って，室内の電器機器に対する電磁干渉の影響を考えずに済むなどの利点が挙げられます． 本研究では，光無線ネットワークにおいて，多元接続方式であるCDMAへの適用について考え，従来の光無線多元接続方式を用いたものよりも，より柔軟なネットワーク構成を作り上げることを目指します．
MIMO
送受信機に複数のアンテナを搭載して通信路容量を増やす多入力他出力(MIMO)方式は，現在無線通信で広く使われていますが， アンテナの数が増えるに連れて最適判定に必要な復号の計算量も指数的に増えてしまいます． また，これらのアンテナを有効に使うための多重化方法もさらなる研究開発が必要となります． 本研究では，主に複数のアンテナを有効に使うためのConstellation Rotated Vector-OFDM(CRV-OFDM)方式での受信方法や位相雑音の影響抑制方法などを研究しています．
CCCC

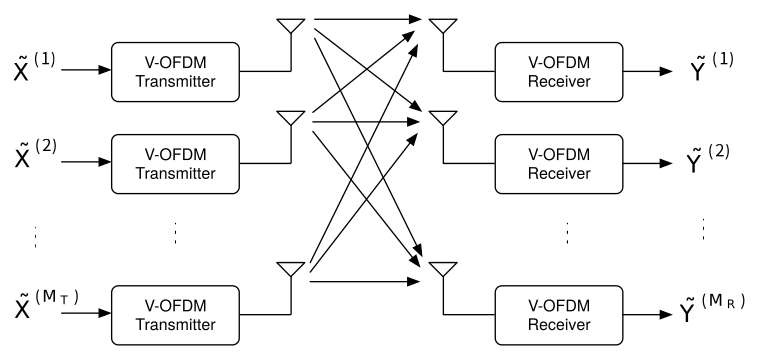
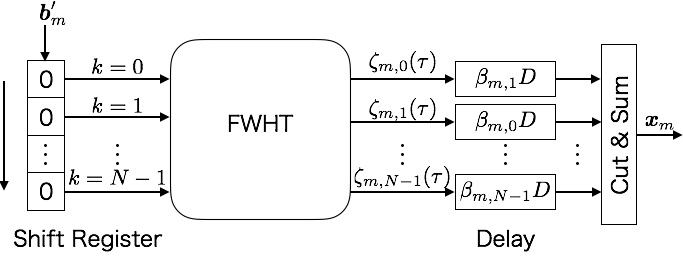
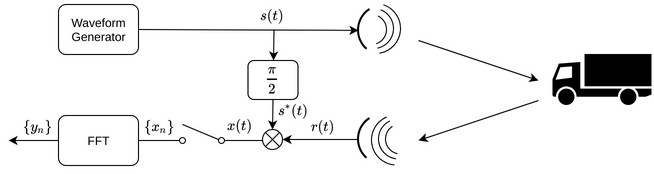
電波を利用して通信を行う無線通信では，周波数及び時間を共有する複数のユーザの無線信号から希望信号を取り出す必要があります． そのときに，送信機から送信された信号は多重反射により強くなったり弱くなったりするフェージングという現象が起こる他， 様々な経路を通って届いた信号は伝達時間が異なるため，送信された信号は時間をずらしながら加算され，送信信号と通信路ベクトルの畳み込みの形式で受信されます．

このような状況で安定した通信を行うためには，送信する信号の波形を上の状況に対応できるように設計する必要がありますが， このテーマでは離散化された送信信号を系列として信号設計を行い，高効率な無線通信システムに使用できる完全相補系列系やzero correlation zone(ZCZ)系列 の構成法及びその実装方法について研究し，性能評価を行います．

第五世代無線通信では，人間だけではなく大量のものを無線で繋げる，非直交多重接続方式(NOMA)が注目されています． NOMAは接続するものに異なる電力を配分するPower-domain NOMAと，非直交符号を割り当てるCode-domain NOMAにわけられますが， このテーマではSparse Code Multiple Access(SCMA)などCode-domain NOMAを主に研究します．
Trap
日本では現在，鹿や猪などの有害鳥獣が増え，農産物被害が年間約200億円になってます． 一方，これらの有害鳥獣を駆除する猟師は高齢化が進み，山の巡回などが困難になってます． 本研究室では，ICTで猟師を支援するために，Low Power Wide Area(LPWA)の通信方式であるLoRaを用いて， 罠に有害樹がかかっているかを検知できる装置を開発してます．
FMCW
周波数変調連続波(Frequency Modulated Continuous Wave:FMCW）レーダーは自動車の自動運転などで周辺の車の位置や移動速度を判定するのに広く使われています． しかし，FMCWレーダーは周辺に複数のターゲットが存在するときに実際には存在しないゴーストターゲットを除去する必要があり，計算量が多くなり位置や速度の判定精度も落ちてしまいます． このテーマでは，ターゲットからの反射信号の振幅情報を利用して計算量が少なく精度の高いターゲット判定の方法を研究します． また，送信機に位相雑音が存在するときに，その影響を抑制する方法に関しても研究を行っています．
RTB
現在ネット広告の規模はテレビ広告を越え，最大の広告媒体となっていますが，ネット広告ではReal Time Bidding(RTB)というビッグデータに基づいた入札方式が使われています． ユーザがサイトにアクセスすると，サイトの広告枠とユーザの情報はAd Exchange(ADX)と呼ばれる広告取引マーケットに送信され， 広告代理店はDemand Side Platform(DSP)で入札を行います． DSPは入札の際に，サイトにアクセスしたユーザが広告をクリックする確率を予想する必要がありますが， そのために過去のアクセスデータから確率モデルを生成します． このテーマでは，確率モデルの生成，関連商品の推薦方法およびプライバシー保護などの問題についての研究を通じて，ビッグデータや人工知能に関する基礎知識を身につけることを目的とします．